药物临床试验非劣效设计指导原则
一、概述
当确证某个药物疗效时,优效试验(如证明试验药与安慰剂或阳性药相比较的优效性)一般是理想选择。当优效试验不适用,比如使用安慰剂对照不符合伦理要求时,可考虑采用非劣效试验。非劣效试验 是为了确证试验药的临床疗效,即使低于阳性对照药,但其差异也是在临床可接受范围之内。
本指导原则旨在阐述非劣效试验的应用条件、设计要点、非劣效界值设定、统计推断以及 其他 监管考虑等方面内容,以指导临床试验各相关方能够正确地认识、实施和评价非劣效试验。本指导原则主要适用于支持药品注册上市的确证性临床试验,也可供探索性临床试验参考使用。
二、应用条件
非劣效试验以阳性药作为对照,目的是确证虽然试验药的疗效低于阳性对照药的疗效,但差异在可接受的范围之内。非劣效试验中阳性对照药相对于安慰剂的疗效无法在本试验中直接观察, 因此需要假定阳性对照药有确切的疗效。非劣效试验应确保具有足够的检定敏感性,即具有区分阳性对照药为有效、低效或无效的能力。关于检定敏感性的详细阐述可参考 ICH E10《临床试验中对照组的选择和相关问题》。
要确保非劣效试验具有一定的敏感性,应着重考虑以下三个方面:
(一)阳性对照药疗效的既往证据
通常阳性对照药相对于安慰剂的疗效差异来源于已知的、具有良好设计和实施的临床试验结果。根据这些既往试验,在充分考虑不同试验结果变异程度的基础上,可以估计出较为可靠的阳性对照药相对于安慰剂的疗效差异,该疗效差异是非 劣效试验中用于确定非劣效界值的关键参数。
对于某些症状性治疗或一些适应症,如精神类适应症等,在既往试验中难以获得阳性对照药相对于安慰剂的稳健疗效差异,若使用该阳性对照药进行非劣效试验,则很难确证试验药的疗效。因此,对于这些疾病领域,谨慎使用非劣效试验,或者在伦理许可的前提下采用包含安慰剂的三臂非劣效试验。
(二)恒定假设
阳性对照药相对于安慰剂的疗效差异估计多源于既往临床试验,因此在非劣效试验中应尽可能确保阳性对照药的疗效与既往临床试验保持一致,即满足恒定假设。恒定假设会受到很多因素的影响,诸如既往试验中的 受试人群、是否有合并用药、疗效指标的定义与判定、阳性对照药的剂量、耐药性以及统计分析方法等。如果随着年代迁移,所治疗疾病的定义、诊断标准及其治疗方法等已经发生变化,则会影响恒定假设的成立,进而导致非劣效试验的检定敏感性不足,难以解释试验结果。因此,当恒定假设难以验证时,谨慎使用非劣效试验。
(三)良好的研究质量
临床试验质量是非劣效试验具有足够的检定敏感性的基础。各种试验质量缺陷,包括偏离方案中规定的入组标准、依从性差、合用影响疗效评价的药物、测量偏倚、分组错误、受试者脱落率高等,都有可能导致试验药与阳性对 照药的疗效差异估计出现偏倚。这些试验质量缺陷在优效试验中通常不利于优效结论成立,但在非劣效试验中却可能有利于非劣效结论成立。因此,在非劣效试验的设计和实施阶段保证研究质量尤为重要。
三、设计要点
临床试验设计时,要考虑试验目的、研究人群、对照选择、评价指标、统计假设、样本量、数据分析和解读方法等要点。对于 其他 指导原则(如 ICH相关指导原则和我国发布的《药物临床试验的生物统计学指导原则》)涉及到的临床试验设计通用内容,在试验设计时应遵循,本指导原则不再赘述。本指导原则着重阐述非劣效试验特有的设计要点,包括统计 假设(其中非劣效界值在第四章中阐述)、阳性对照药的选择和分析人群。
(一)统计假设
试验方案中应明确非劣效统计假设。对于不同度量和指标类型,非劣效试验统计假设的表述会有所不同,见表 1。原假设(H0)对应为劣效,备择假设(H1)对应为非劣效M为非劣效界值,绝对度量指标包括均值差和率差等,相对度量指标包括率比、风险比、比值比等,高优指标是其值越大表明疗效越好的指标,低优指标是其值越小表明疗效越好的指标。
表1 非劣效试验的原假设(H0)和备择假设(H1)
| 指标类型 | 高优指标 | 低优指标 |
|---|---|---|
| 绝对度量 |
H0:T − C ≤ −M(M>0) H1:T − C > −M(M>0) |
H0:T − C ≥ M(M>0) H1:T − C < M(M>0) |
| 相对度量 |
H0:T/C ≤ 1/M(M>1) H1:T/C > 1/M(M>1) |
H0:T/C ≥ 1/M(M>1) H1:T/C < 1/M(M>1) |
| T代表试验组效应, C代表阳性对照组效应, M代表非劣效界值。 | ||
(二)阳性对照药
非劣效试验所选择的阳性对照药必须具有其疗效优于安慰剂的明确和充分的证据,包括可靠的疗效差异估计。阳性对照药应选择当前 标准疗法或者最佳疗法的药物。如果所选的阳性对照药的疗效证据不充分,那么将其用于评价 其他新药疗效会存在巨大风险。
(三)分析人群
优效试验基于意向性治疗原则进行统计分析通常被认为是保守的,但应用于非劣效试验则不一定保守。一些试验质量问题,如依从性差、脱落率高、主要终点错误分类等,可能会掩盖试验组和对照组之间的治疗差异,从而导致实际上比对照药劣效的试验药错误的获得非劣效于对照药的结论。另一方面,受试者是否遵守试验方案可能与接受何种药
另一方面,受试者是否遵守试验方案可能与接受何种药物和治疗的结果有关,因此按符合 方案集进行分析也可能引入偏倚。比如要评价能够耐受并继续接受治疗的受试者的疗效,符合方案集未必反映了不同治疗方案下相似的受试者。任何按符合方案集进行的分析都应针对临床所关注的人群的疗效,确认是由于治疗而不是潜在的混杂因素(例如观察时间或患者特征的差异等)引起的效应。
建议在非劣效试验设计阶段就应该重视研究质量,并且在实施和分析阶段持续的监测以减少发生上述质量问题。如果非劣效试验是开放试验,由于很难证明试验入组、终点评估以及其他研究操作未引入偏倚,所以关注研究质量就更为重要。
四、非劣效界值确定与统计推断
非劣效界值是指试验药与阳性对照药相比在临床上可接受的最大疗效损失。因此,非劣效界值不应大于阳性对照药相对于安慰剂的临床获益,以确保试验药的疗效至少能够优于安慰剂。非劣效界值的确定通常应根据统计分析和临床判断综合考虑,并在试验方案中说明非劣效界值确定的依据。
非劣效界值的确定及其统计推断主要包括固定界值法和综合法,一般情况下固定界值法可以更直观地描述试验药物的疗效。
(一)固定界值法
阳性对照药与安慰剂的疗效差异用M1表示,其估计通常依赖于既往阳性对照药与安慰剂的优效试验的疗效差异的meta分析,通过分析得到疗效差异的单侧97.5%(或双侧95%)置信区间。M1的确定方法详见图1和图2。如果对既往证据的变异性和恒定假设存在顾虑可采用 “折扣 ”策略确定M1即将M1通过一定幅度的 “折扣”(如减半)转换为更加保守的M1。
非劣效界值M2(对应于前文表1中的M)是试验药与阳性对照药相比在临床上可接受的最大损失,可通过M1的某一比例来定义。设f(0< f<1)为至少保留M1的比例,则最大可损失比例为1-f。M2的确定公式详见附录2,M1和M2的相对关系参见图1和图2。确定f则依赖于临床判断。当阳 性对照药与安慰剂的疗效差异很大时,或当终点指标为不可逆的发病率或死亡率时,对f的选择应该慎重考虑。
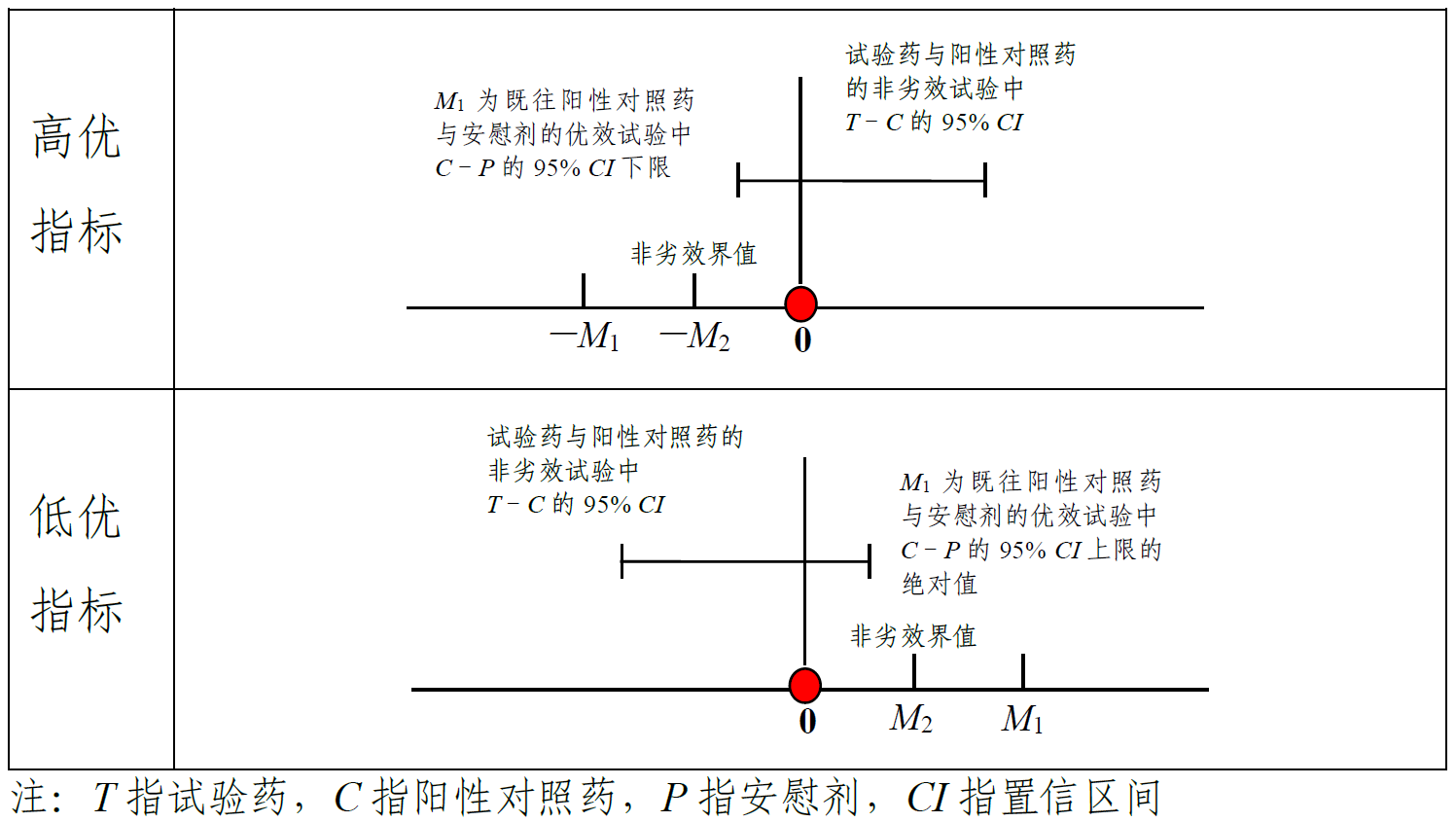
图1 绝对度量指标的非劣效界值确定过程图示
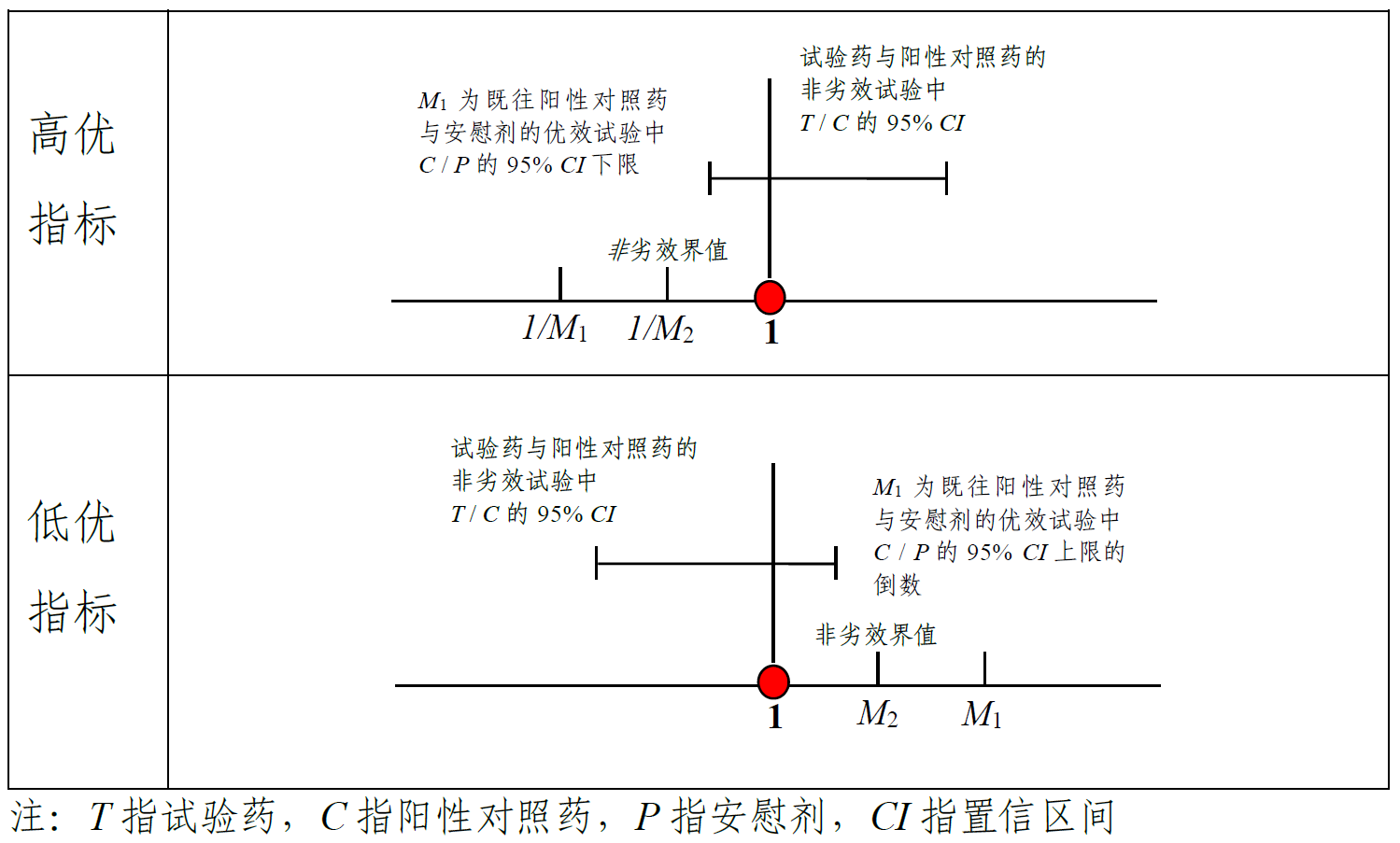
图2 相对度量指标的非劣效界值确定过程图示
若检验水准α设为单侧0.025或双侧0.05,对于高优疗效评价指标,若为绝对度量值,而试验药相对于阳性对照药的疗效差异的单侧97.5%(或双侧95%)置信区间的下限大于负的非劣效界值(若为相对度量值,下限大于非劣效界值的倒数),则可推断试验的非劣效结论成立;对于低优疗效评价指标,无论是绝对度量值还是相对度量值,如果试验药相对于阳性对照药的疗效差异的单侧97.5%(或双侧置信区间的上限小于非劣效界值,则可推断试验的非劣效结论成立。
(二)综合法
综合法不要求预先确定M1,而是将既往阳性对照药与安慰剂的优效试验和当前试验药与阳性对照药的非劣效试验的数据进行合并或综合,构建一个检验统计量Z来表达试验药是否保留了阳性对照药疗效的一部分。检验统计量Z的计 算公式详见附录2。如果用Z1-α/2表示标准正态分布的100(1-α/2)%百分位数,对于高优疗效评价指标,若 Z大于Z1-α/2,或对于低优疗效评价指标,若Z小于Z1-α/2,则可推断试验药非劣效于阳性对照药。
只要恒定假设成立,使用综合法相对于使用固定界值法可以提高研究效率(减少样本量或样本量不变而获得更大的检验效能);综合法虽然在开展非劣效试验之前不需要预先确定M1,但需要在方案中基于临床判断预先确定f值。
五、其他考虑
(一)相对于疗效损失的潜在获益非劣
非劣效设计允许试验药疗效相对于阳性对照药有一定的损失,相应地也要考虑试验药在 其他方面是否有潜在获益,以对其疗效损失进行必要补偿。例如,与阳性对照药相比,其他方面的潜在获益可能包括疗程更短、使用更方便、不良反应更少、依从性更好等。对潜在获益的评估应综合考虑非劣效试验目的和关注的临床问题。
(二)非劣效与优效检验的转换
在非劣效试验方案中可以预先定义非劣效与优效检验的转换,即先进行非劣效检验,如果非劣效结论成立,可进一步进行优效检验,如果优效结论成立,则研究结论为优效;如果优效结论不成立,则研究结论为非劣效。当非劣效结论不成立时,研究结论不支持非劣效,也不应再进行优效检验。
若计划在采用阳性对照药的优效检验不成立时进行非劣效检验,则须在试验方案中预先考虑优效与非劣效检验的转换,包括事先定义非劣效检验假设、非劣效界值,以及多重性校正的策略等。
(三)三臂非劣效设计
为了考察试验药是否非劣效于阳性对照药,还可以考虑包含试验组、阳性对照组和安慰剂组的三臂非劣效设计,前提条件是符合伦理。三臂非劣效设计在检验试验药非劣效于阳性对照药的同时,还可以考察阳性对照药是否优效于安慰剂,从而在临床试验内部建立确切的检定敏感性。因此,在伦理许可的情况下,三臂非劣效设计是确证试验药非劣效于阳性对照药的较理想的试验设计。
(四)与监管机构的沟通
当申请人计划采用非劣效试验时,鼓励与监管机构及时沟通。沟通的问题包括但不限于阳性对照药的选择、非劣效界值的确定、主要分析人群、非劣效与优效检验的转换 、替代设计的考虑等问题。进行沟通前,申请人应该向监管机构预先提供包含统计分析考虑的试验方案等相关资料。例如,在沟通非劣效界值时,申请人应预先提供确定非劣效界值的详细过程,包括所用到的文献及meta分析结果等。
附录:中英文词汇对照
| 中文 | 英文 |
|---|---|
| 检定敏感性 | assay sensitivity |
| 非劣效界值 | non-inferiority margin |
| 恒定假设 | constancy assumption |
| 固定界值法 | fixed margin method |
| 综合法 | synthesis method |
| 人用药品注册技术要求国际协调会议 | the International Conference on Harmonisation of Technical Requirements for Registration of Pharmaceuticals for Human Use, ICH |
| 意向性治疗 | intention-to-treat, ITT |
| 符合方案集 | per protocol set, PPS |
附录:主要公式
(一)固定界值法
若M1为绝对度量,则
若M1为相对度量,则
(二)综合法
对于绝对度量的疗效评价,
对于相对度量的疗效评价,
公式中,Ch和P分别为既往优效试验中阳性对照药和安慰剂的效应;T和Cn分别是当前非劣效试验中试验药和阳性对照药的效应;f为根据预先确定的Ch相对于P的疗效差异的所保留的比例;SE为标准误,既往优效试验的SE需要根据阳性对照药相对于安慰剂的疗效差异的meta分析进行估计。此处相对度量以简单比值(如相对风险)示例。某些相对度量值(如通过等比例风险模型估计的风险比)在大多数情况下并不能表示为简单比值,但可同理推导。
附录:应用示例
(一)固定界值法
以一项用于评估新型抗凝血剂希美加群与阳性对照药华法林的非劣效试验 为例。华法林是一种高效的口服活性抗凝剂,已被批准用于治疗具有血栓栓塞并发症风险的非瓣膜性心房颤动患者。1989年至1993年发表了六项华法林用于治疗非瓣膜性心房颤动患者的安慰剂对照试验,主要试验结果汇总于附表 1,为评估希美加群与华法林的非劣效试验确定非劣效界值提供基础。
附表1 华法林用于治疗非瓣膜性心房颤动的安慰剂对照试验
| 试验 | 概要 | 华法林 | 安慰剂 | 华法林与安慰剂的相对风险(95% CI) |
|---|---|---|---|---|
| AFASAK | 开放,1.2年随访 | 9/413 = 2.18% | 21/398 = 5.28% | 0.41 (0.19, 0.89) |
| BAATAF | 开放,2.2年随访 | 3/487 = 0.62% | 13/435 = 2.99% | 0.21 (0.06, 0.72) |
| EAFT | 开放,2.3年随访 | 21/507 = 4.14% | 54/405 = 13.3% | 0.31 (0.19, 0.51) |
| CAFA | 双盲,1.3年随访 | 7/237 = 2.95% | 11/241 = 4.56% | 0.65 (0.26, 1.64) |
| SPAFI | 开放,1.3年随访 | 8/260 = 3.08% | 20/244 = 8.20% | 0.38 (0.17, 0.84) |
| SPINAF | 双盲,1.7年随访 | 9/489 = 1.84% | 24/483 = 4.97% | 0.37 (0.17, 0.79) |
将上述六项试验结果合并进行固定效应meta分析,华法林相对于安慰剂的相对风险点估计值为0.361,95%置信区间(CI)为(0.267,0.489)。由于该主要评价指标为低优指标,因此,M1为95%CI上限的倒数,即1/0.489=2.04。
本项非劣效试验的主要目的是证明希美加群保留了华法林相当大一部分疗效,因此f至少为50%,则代表在对数风险尺度上最大可接受的非劣效水平为(1−50%)ln(M1),根据公式进行指数变换计算出M2为1.43。
在希美加群与华法林的非劣效试验中,考虑到试验的主要评价指标为低优指标,希美加群相对于华法林的相对风险为1.39,95% CI为(0.91,2.12),其上限大于M2。因此,根据该试验结果尚不能认为希美加群降低风险的作用非劣效于华法林。
(二)综合法
继续以上述试验为例。综合法比较了当前非劣效试验中希美加群相对于既往华法林与安慰剂的优效试验中安慰剂的疗效,这是一种不基于在当前试验中设置安慰剂组的间接比较。综合法将既往华法林与安慰剂的优效试验的数据与当前希美加群与华法林的非劣效试验的数据合并进行假设检验,证明在非劣效试验中保留了一定比例的华法林相对于安慰剂的疗效。
综合法有别于固定界值法的关键点在于不需要在开展当前非劣效试验之前预先确定华法林相对于安慰剂的疗效M1)。虽然在当前非劣效试验中并不对华法林与安慰剂进行比较,但其前提假设是,当前非劣效试验中华法林与安慰剂之间的疗效差异(如果有的话)与既往华法林与安慰剂的优效试验所观察到的疗效差异相同。
在此基础上,综合法在统计上检验原假设,即希美加群与华法林相比,其劣效性低于华法林与安慰剂相比风险降低的一半(即预设 50%)。这是固定界值法不能直接解决的问题,因为在固定界值法中,安慰剂仅存在于既往试验中,而不存在于当前非劣效试验中。在对数(log)风险尺度上进行检验,其原假设H0为:
ln(希美加群与华法林的相对风险) ≥ -0.5 ln(华法林与安慰剂的相对风险)
在非劣效试验中,希美加群与华法林的相对风险为1.39,95% CI为(0.91,2.12)。从便于解释的角度,以固定界值法中meta分析结果为参考,华法林与安慰剂的相对风险为0.361,95% CI为(0.267,0.489)。基于此,希美加群相对于华法林的相对风险点估计值在对数尺度上为0.329,即ln(1.39),标准误为 0.216,而华法林相对于安慰剂的相对风险点估计值在相应的对数尺度上为-1.02,即ln(0.361),标准误为0.154。
根据综合法的统计检验公式有:
其Z大于-1.96,据此推断该试验结果尚不能认为希美加群非劣于华法林。
