物料消耗模拟器用户指南

English Version

User Manual for Materials Consumption Simulator

物料消耗模拟器

1. 为什么模拟

1.1. 基础场景C₀

想象一下，你是一名项目经理（PM），负责监督一项单中心随机对照试验（RCT）。

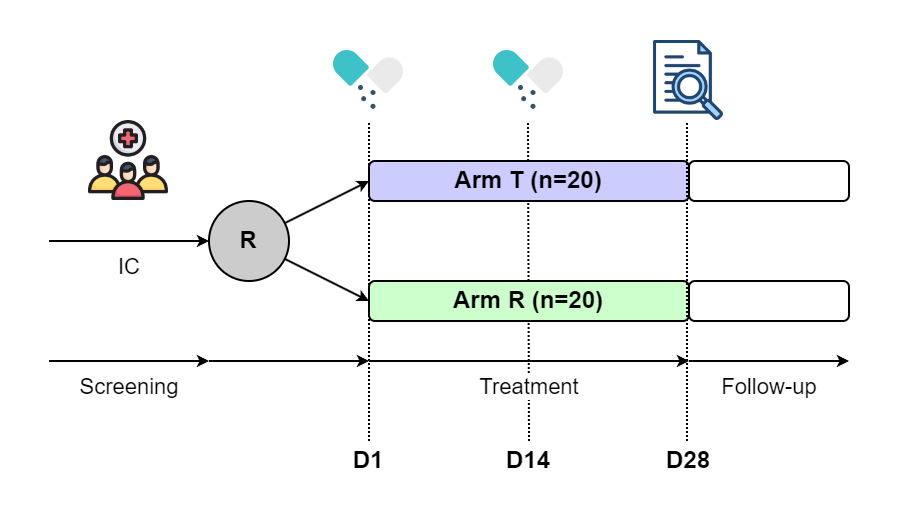
Figure 1. Base Scenario C₀

试验方案规定，符合纳入和排除标准的40名患者将被随机分为两个治疗组：T组和R组，分配比例为1:1。每位患者将收到两套研究物料，一套在第1天，一套是在第14天。

研究物料的理论消耗量相对容易计算：

T组：

20例患者 × 2个套/患者（第1天和第14天）= 40套

R组：

20例患者 × 2个套/患者（第1天和第14天）= 40套

由于这是一项单中心试验，作为项目经理，确保将正确数量的物料运送到现场相对简单。在这种情况下，您可以证明至少应向中心运送40套T和40套R，以满足预期的消耗。但是，为了考虑潜在的不可预见的情况，您决定添加一个小缓冲区。根据您的经验和历史数据，由于以下各种因素，您预计重新分配的可能性为5%：

物料损坏

装运过程中的损失

患者不依从或给药错误

为了降低物料料用完的风险，您决定为每个组额外运送原始所需数量的5%。这导致T组有42套，R组有42套。

C₀是一个清楚的例子，说明在具有简单物流和可预测需求的试验中，手动方法就足够了，使得基本物料供应计划不需要模拟。

1.2. 升级方案C_center=2

你面临着提前时间表的巨大压力。为了加速患者的招募，您决定将单中心随机对照试验扩展到多中心随机对照试验。现在，您需要管理两个中心。关键问题变成了：

如何预测多个中心（如C_center=2）的物料消耗?

让我们分解一下你可能面临的问题和挑战：

中心随机化和患者入组分布

在中心随机化的框架下，患者被随机分配到T组或R组。由于所有中心的患者总数固定为40人，这两个中心有41种可能的入组结果——从0到40名患者在中心1入组，其余患者分配到中心2。每种结果都会导致两个中心每组的患者组合不同。

物料要求的不确定性

鉴于患者在各个中心的分布存在不确定性，准确预测每个中心应该运送多少物料是一项挑战。

最简单、最保守的方法可能是向两个中心发送40套T和40套R。然而，这会导致中心的库存过剩。总物料消耗量最终可能达到理论量的200%，这将大大增加成本和资源浪费，这是一个不可接受的结果。

为了避免库存过剩并减少不必要的浪费，您可以考虑另一种策略：向每个中心运送30套T和30套R。这确保了物料的分配更加合理，消耗量将增加到理论消耗量的150%（而不是200%）。虽然这种方法仍然超过了所需的最低限度，但它提供了一种更平衡的解决方案，在不过度积压的情况下覆盖了患者登记的潜在变化。

在真实世界

您可以考虑采用更具适应性的运输策略，而不是一次性运输所有物料。这允许您根据每个中心随时间推移的实际注册状态调整物料发货，从而降低物料积压或用完的风险。以下是它的工作原理：

首次供应：根据最初的患者预期，您向每个中心运送的物料数量较少，例如，向每个中心发送10套T和10套R。这考虑到了早期患者登记，并确保您不会积压。
补充供应：随着患者登记的进展，您将监控每个中心的实际消耗量。当库存水平降至某个阈值以下时，会触发新的发货。阈值是确保您在两次发货之间不会用完物料的最低库存水平。

当然，你需要定义以下参数：

第一批货物应向每个中心运送多少套物料？

触发后续发货的库存阈值是多少？

后续装运应装运多少个套物料？

1.3. 模拟

这就是模拟变得无价的地方。通过使用模拟，您不再需要依赖简单的确定性计算。该模拟可以解释患者将如何在各个中心分布以及材料将如何消耗的不确定性。通过这种方法，您可以确定最佳的供应策略，以平衡确保充足供应的需求，同时避免过度积压或缺货。您可以做出数据驱动的决策，以提高临床试验物流的准确性和效率。

在这个阶段，我们了解到，深入了解如何进行模拟的细节可能会让人感到不知所措，因此我们将专注于直接呈现关键的评估结果：

Table 1. 多种供应策略

#	供应策略	成功率	理论消耗量	实际消耗量	膨胀率
1	单次转运40套T和40套R	100%	40套T和40套R	80套T和80套R	200.0%
2	单次转运30套T和30套R	99%	40套T和40套R	60套T和60套R	150.0%
3	多次转运，首次20套T和20套R 当任意库存低于5时补充5套T和5套R	99%	40套T和40套R	57套T和57套R	142.5%
4	多次转运，首次10套T和10套R 当任意库存低于5时补充5套T和5套R	98%	40套T和40套R	55套T和55套R	137.5%
5	多次转运，首次20套T和20套R 当任意库存低于5时按需补充	96%	40套T和40套R	50套T和50套R	122.5%

简短的回答是，方案4或方案5是最推荐的选择，实际物料消耗量预计在理论消耗量的123%至138%之间。这个范围提供了对所需物料的更现实的估计，并且比准备150%甚至200%的物料更有效，这会导致库存过剩和不必要的成本。

在以下部分中，MACROLIB将引导您了解用于模拟材料消耗的蒙特卡洛模拟的基本机制。我们将介绍：

模拟的工作原理：详细解释蒙特卡洛方法及其如何应用于预测各种试验场景中的材料使用情况。

设置模拟：关于如何定义和证明模拟参数以确保准确预测特定试验需求的实用指南。

解释结果：逐步解释如何解释模拟的输出，包括对结果对您的材料供应策略意味着什么的见解。

最后，我们将介绍仓库：一组真实场景和模拟结果的示例。这些示例将作为参考，帮助您更好地理解如何在不同的试验环境中应用模拟。

2. 如何模拟

这里有一个快速简单的版本，可以帮助你向同事解释这个想法，而不会陷入技术细节：

MACROLIB利用蒙特卡洛模拟通过对不同场景进行多次迭代来了解不确定性对预测的影响。每次迭代都是一次试运行，随机调整变量，模拟不同的可能结果。

通过多次重复这些模拟（通常是数千次迭代），而不是依赖于单一的、可能不准确的估计，你会得到一系列可能的结果，这有助于你做出更明智的决定——你不仅仅是猜测；证据基于广泛的潜在情景。

如果你是那种喜欢深入了解技术细节并真正了解其工作原理的人，别担心——我们已经为你做好了准备。以下部分将用简单的英语分解蒙特卡洛模拟过程，因此即使你没有统计学背景，你仍然可以跟随并牢牢掌握模拟的工作原理以及如何解释结果。

2.1. 目标函数

稳健的物料供应策略应主要解决以下问题：

确定最优供应策略-库存和积压之间的平衡。

一方面是确保每个中心都有足够的库存，以满足患者在领取研究材料时的需求。这对于保持试验的完整性至关重要，因为不按照方案分配材料可能会产生严重后果。

然而，另一方正在避免中心库存过剩。虽然确保有足够的库存是至关重要的，但库存过剩同样可能造成问题。中心库存水平过高会导致浪费和效率低下。

此外，根据具体情况，应仔细排除其他因素：

对于具有严格存储条件的产品（例如，需要温度控制或湿度调节的产品），最佳策略可能是尽量减少装运次数，以降低存储管理的复杂性。

对于保质期较短的产品，最佳策略可能侧重于在任何给定时间将库存水平降至最低。其目的是避免大量材料在库存中存放太久，从而降低库存过期的风险。

在每种情况下，优化都是关于平衡可用性、成本、存储复杂性和产品生命周期之间的权衡。根据具体的产品和试验要求，最佳策略可能会优先考虑这些因素中的一个或多个。

2.2. 复杂系统

在现实世界中，临床供应链并不是孤立运作的。它们是由不断相互作用的多个维度形成的。

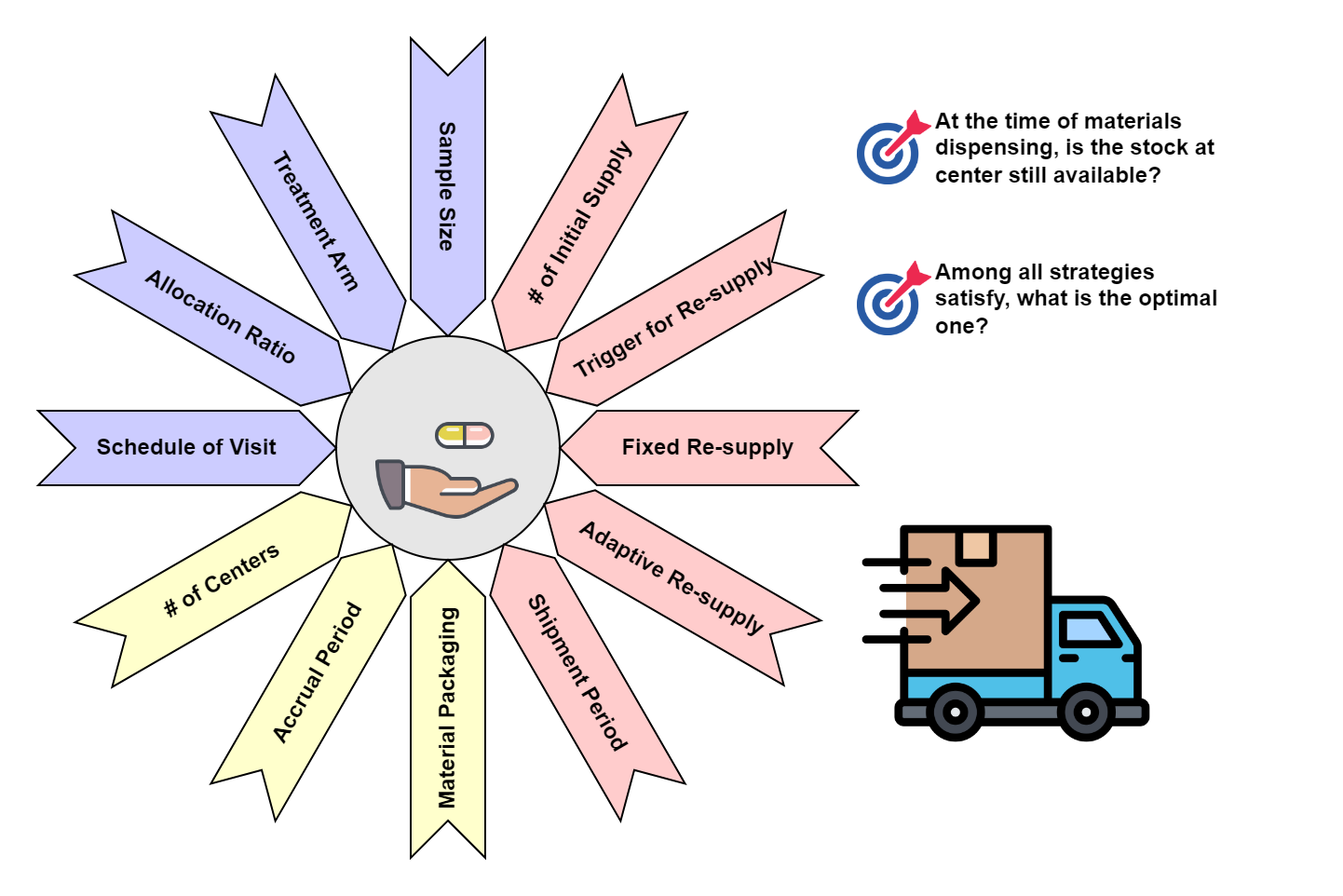
Figure 3. Complex System for Clinical Trial Material Supply

这些维度包括：

试验设计是直接影响供应计划的基础维度。正如我们在第1.1节中讨论的那样，物料的理论消耗量来自样本量、治疗组分配和就诊时间表等因素。这些因素在计算试验所需物料的基本量时至关重要。

后勤在确定供应策略方面也起着至关重要的作用。在第1.2节中，我们说明了添加另一个中心如何影响物料分布。但是后勤不仅仅是场地的数量。其他因素，如患者入组率、运输时间和库存周转率，也带来了复杂性。

一旦试验设计和物流都完成，就可以制定供应策略，以确保在正确的时间提供适量的物料。我们可以应用不同的策略来管理材料分配和补给。例如，表1（本节稍后提供）说明了多中心试验的各种供应策略（C_center=2）

以供应策略#4为例：

在这种情况下，整个试验过程中计划进行多次转运。第一批物料向每个中心发送10套T和10套R。一旦中心的物料被消耗，重新供应的触发器就会被激活。触发器设置为5套（T或R），这意味着当库存降至5套以下时，会触发重新供应。再供应过程如下：

当库存达到5套的再供应阈值时，开始发货。

每批再供应物料包括5套T和5套R，供有需要的中心使用。

这种重新供应在3天内到达，确保中心有他们继续分配所需的物料，不会中断。

2.3. 蒙特卡洛模拟

现在，我们可以执行蒙特卡洛程序来评估复杂系统：

创建一组患者，根据随机化计划分配治疗组，模拟入组日期和随后的配药日期；

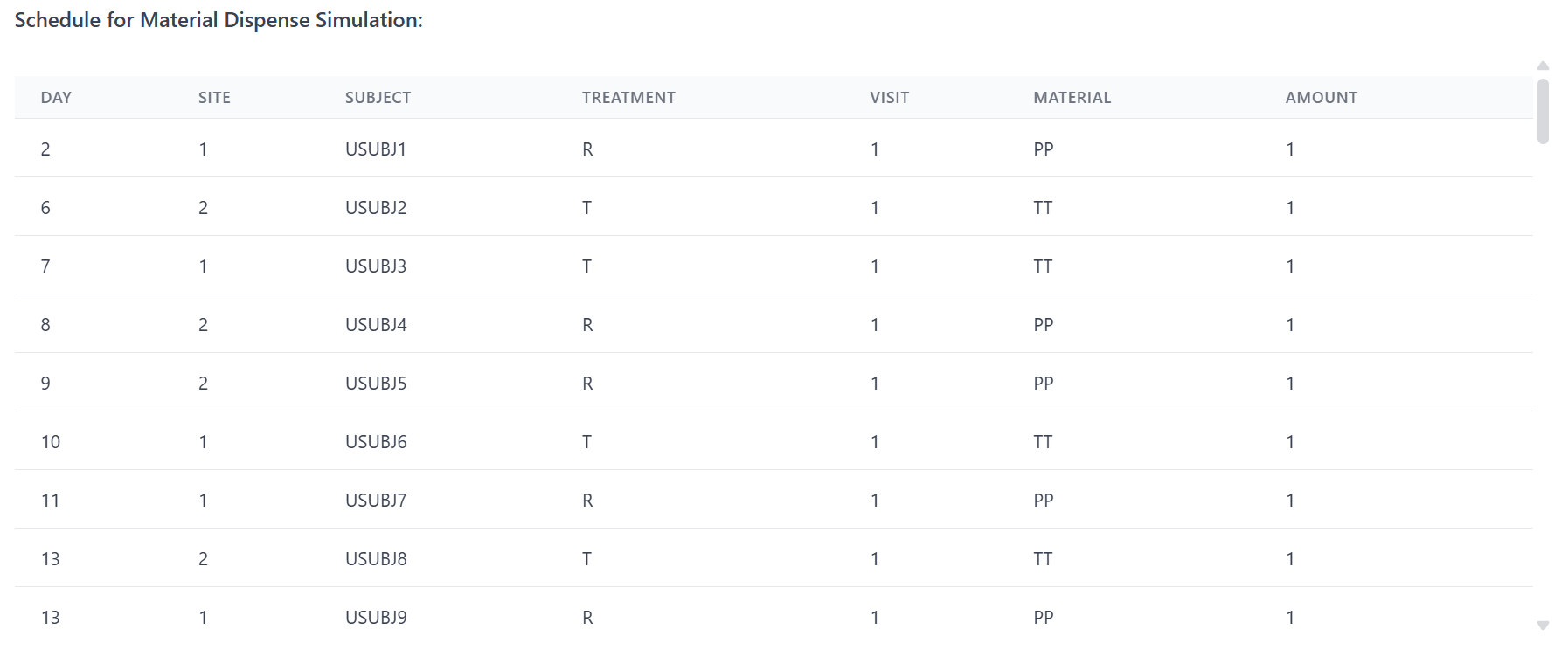
Figure 4. 蒙特卡罗模拟步骤A

创建一组中心，根据供应策略添加初始供应；

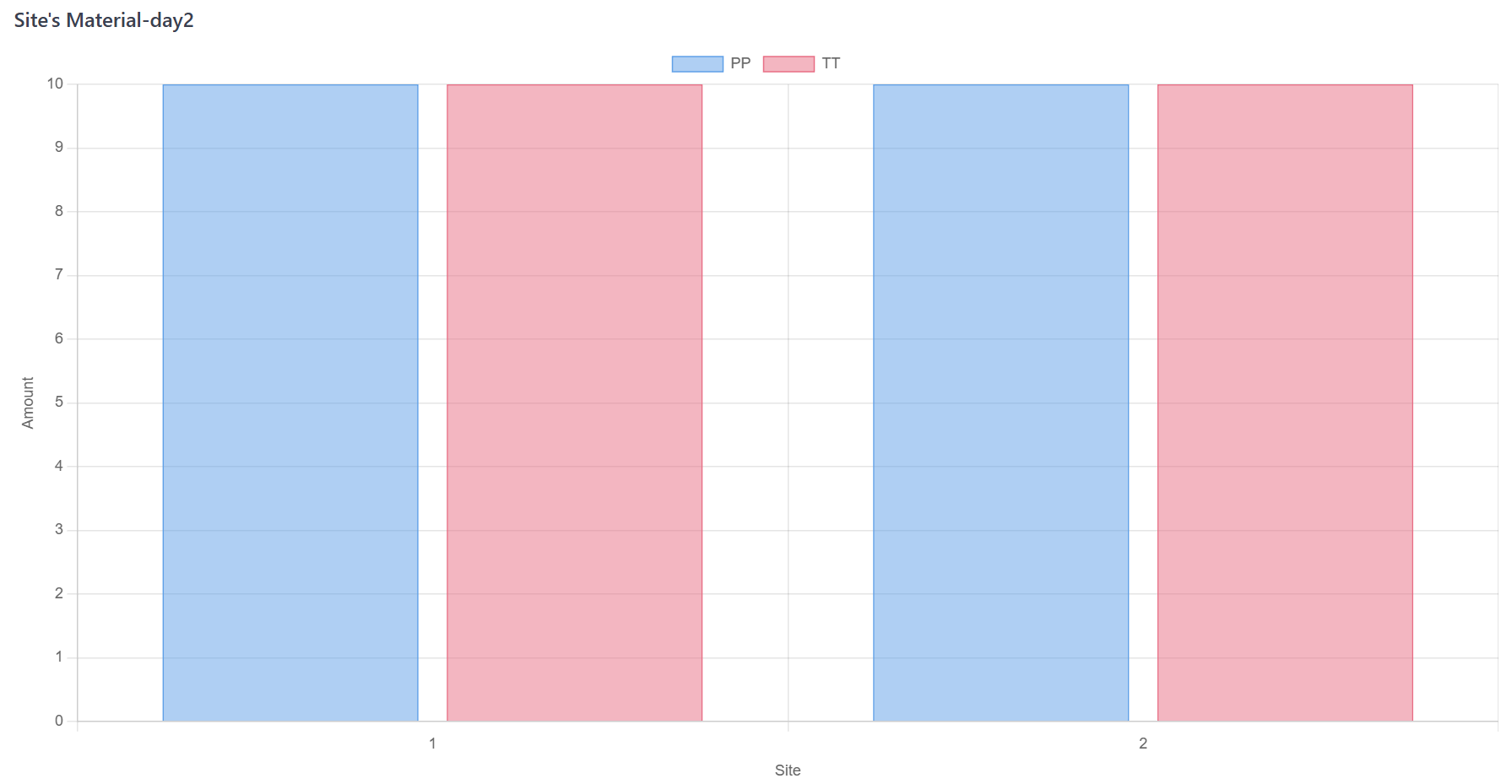
Figure 5. 蒙特卡罗模拟步骤B

一天一天推进试验，根据参观时间表发放材料；

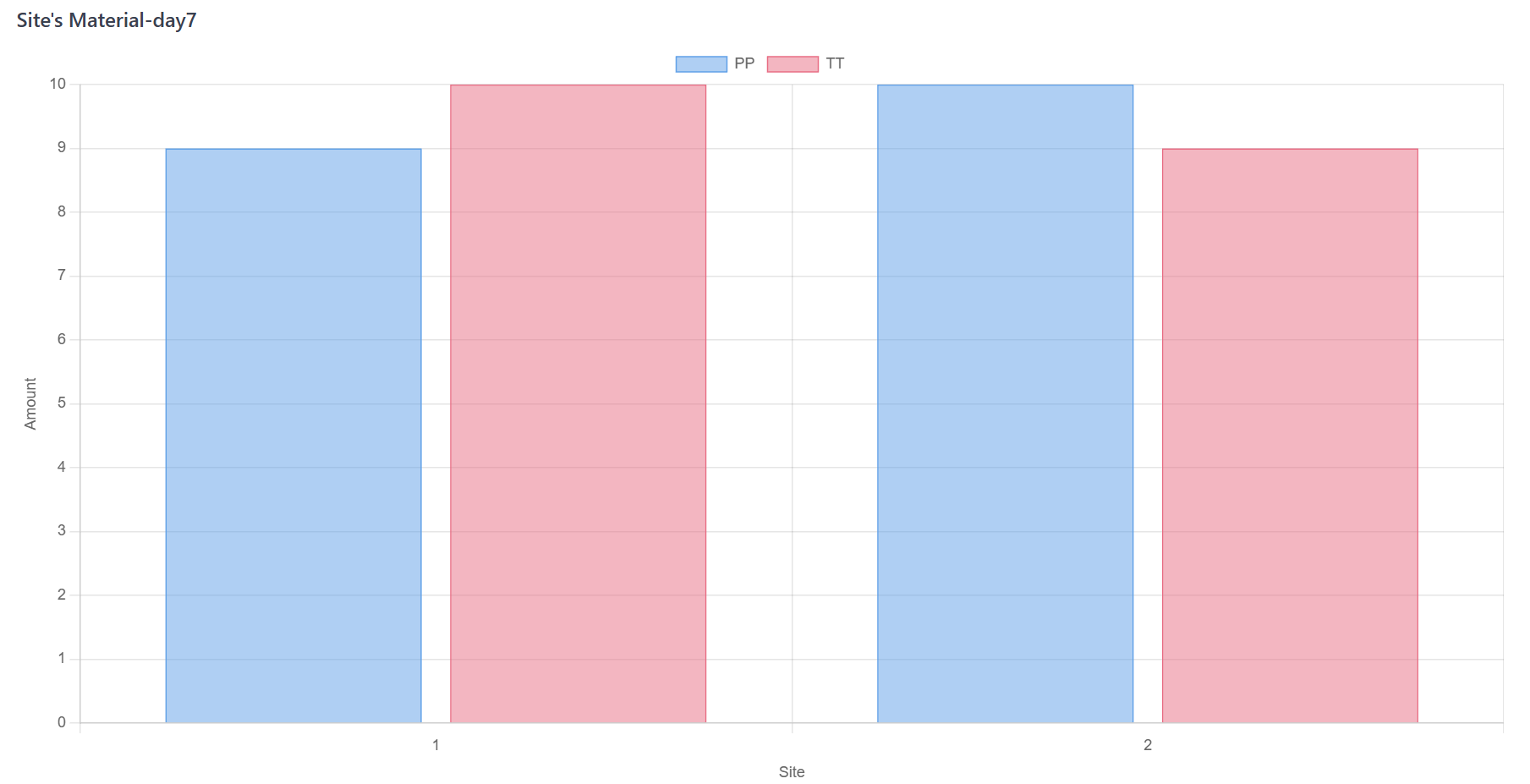
Figure 6. 蒙特卡罗模拟步骤C

每次分发物料后检查库存。如果库存低于预先指定的阈值，则触发重新供应。物料将在转运期后被补充；

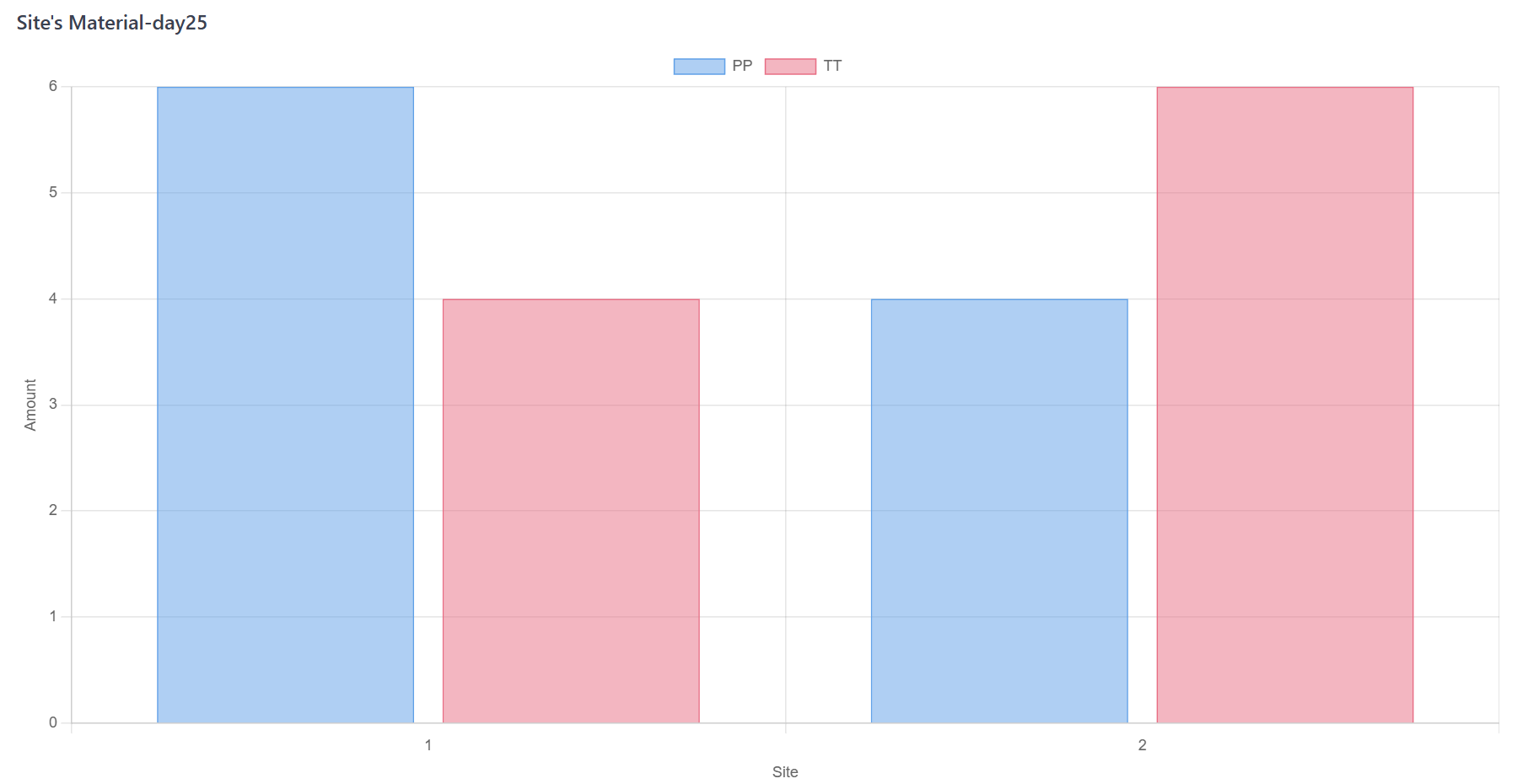
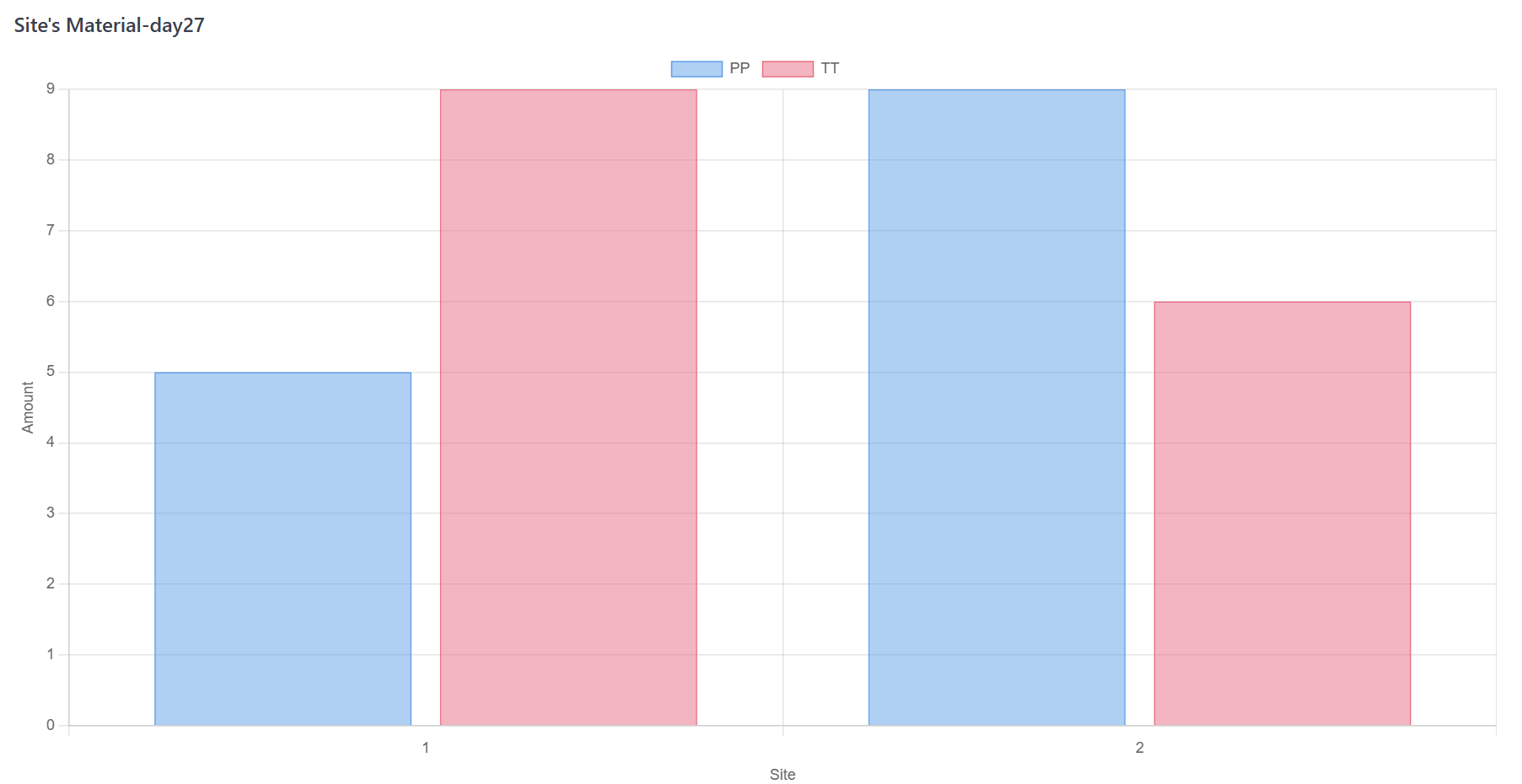
Figure 7. 蒙特卡罗模拟步骤D

试运行到最后。任何中心未能分配物料时，这一次模拟都将被记录为失败。否则，将记录实际供应数量（初始供应和重新供应）；

重复A到E的一定次数，稳定模拟结果。

3. 参数规格

Figure 8 显示了模拟器的输入面板。

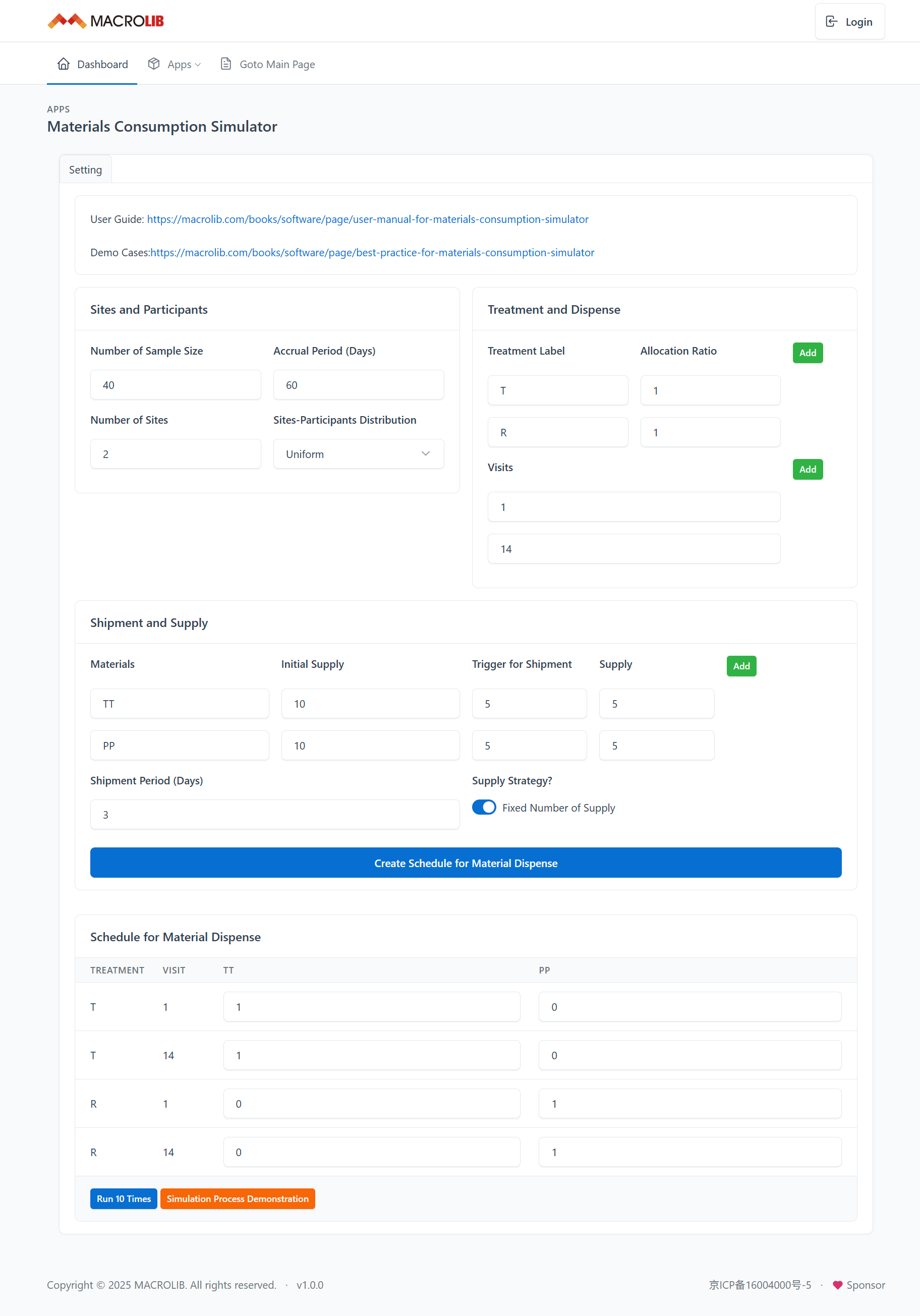
Figure 8. 输入面板

3.1. 试验设计

试验方案提供了构成模拟基础的关键信息。从方案中提取以下关键参数：

样本量是指参与临床试验的患者总数。这对于确定试验的总体规模至关重要，并有助于估算材料供应。

该方案通常定义了治疗组的数量和每个治疗组的分配比率。这种分配比率对于模拟不同治疗组之间如何分配资源和材料至关重要。必须将该比率纳入模拟中，以准确预测材料需求和资源分布。

Table 2. 治疗标签和分配比例示例

试验方案		输入版面
治疗组	分配比例	治疗组	分配比例
Example 1: 安慰剂对照
试验组	2	T	2
安慰剂组	1	P	1
Example 2: 剂量探索
安慰剂组	1	P	1
低剂量组	1	L	1
中剂量组	1	M	1
高剂量组	1	H	1

访问时间表是另一个重要参数。它概述了患者在整个试验过程中预计何时访问临床中心。然而，在许多情况下，并非所有访问都需要分发材料。为了简化模拟，您可以通过只关注发生材料分配的访问来简化时间表。例如：如果患者需要每周到中心进行一次监测，但每月只发放一次材料，则可以调整模拟中的就诊时间表，使其仅反映每月的配药就诊，而不是每周就诊。这种简化有助于降低模拟中不必要的复杂性，同时确保准确捕获材料分配事件。

3.2. 后勤因素

后勤因素虽然很少直接出现在试验方案中，但对模拟结果有重大影响。这些因素在决定如何在整个试验过程中处理和分配物料方面起着至关重要的作用。

物料包装是试验物流中一个关键但经常被忽视的组成部分。

物料的包装和分发模式可以在物料供应方面创造完全不同的场景。例如，包装尺寸的变化会显著影响中心的供应管理和分配方式。这些变化反过来会影响物料的可用性，从而可能影响研究质量。

此外，中心数量和入组期（患者入组的持续时间）是直接影响患者入组率的关键逻辑因素，从而影响物料分配过程。中心的数量决定了试验在地理上的分布范围，并可能影响患者的入组速度。同样，应计期规定了招募参与者的时间，这反过来又影响了何时需要分发和补充物料。

通过考虑这些后勤要素，MACROLIB确保模拟反映了更真实的现实世界场景。这可以更准确地估计物料需求，并有助于规划审判执行的资源和时间表。

3.3. 供应策略

供应策略是指在整个临床试验过程中用于管理物料流动的程序。它确保在正确的时间和地点提供正确数量的物料，优化资源使用，降低短缺或积压的风险。该策略分为三个主要部分：初始供应、再供应触发和再供应。

3.3.1. 初始供应

初始供应是指在临床试验开始时需要提供的物料量，以确保患者入组和治疗顺利开始。

3.3.2. 再供应触发

再供应触发器定义了需要将额外物料运送到临床试验地点的时间点。当临床站点的库存达到预定义的最低水平时，会触发装运以补充站点的库存。发货可能需要时间，以确保在库存不足之前提前发送材料。

3.3.3. 再供应

再供应是指在临床试验过程中在临床试验现场重新进货的过程，以确保所需物品的持续可用性。主要有两种模式：

固定量再供应

用户可以在系统中定义固定数量的再供应。当有可预测的供应需求或物流团队希望保持一致的运输时间表时，这种方法可能很有用。

适应性再供应

或者，大多数材料供应系统（IRT）可以根据当前的库存水平和未来的使用预测自动计算需要补充多少材料。这种方法动态调整再供应量。

适应性再供应有助于确保临床机构在正确的时间补充正确数量的材料，防止短缺和库存过剩。

3.4. 模拟次数

为确保模拟结果的可靠性和稳定性，MACROLIB建议每次模拟至少进行100次迭代。这有助于稳定结果，并减少数据随机波动引起的潜在可变性。虽然100次迭代是一般精度的最低建议，但你运行的迭代次数越多，结果的可靠性就越高。

然而，由于当前的资源限制，默认情况下，MACROLIB仅提供10次迭代的模拟选项。这个有限的数量适用于基本的探索性分析，但可能无法提供更复杂的模拟所需的全部精度。

对于需要更密集模拟或更高迭代次数的用户，我们建议您联系帮助台。我们的团队可以协助提供符合您特定模拟需求和资源要求的定制解决方案。

4. Intepretation

Figure 9 presents the output panel for Simulator.

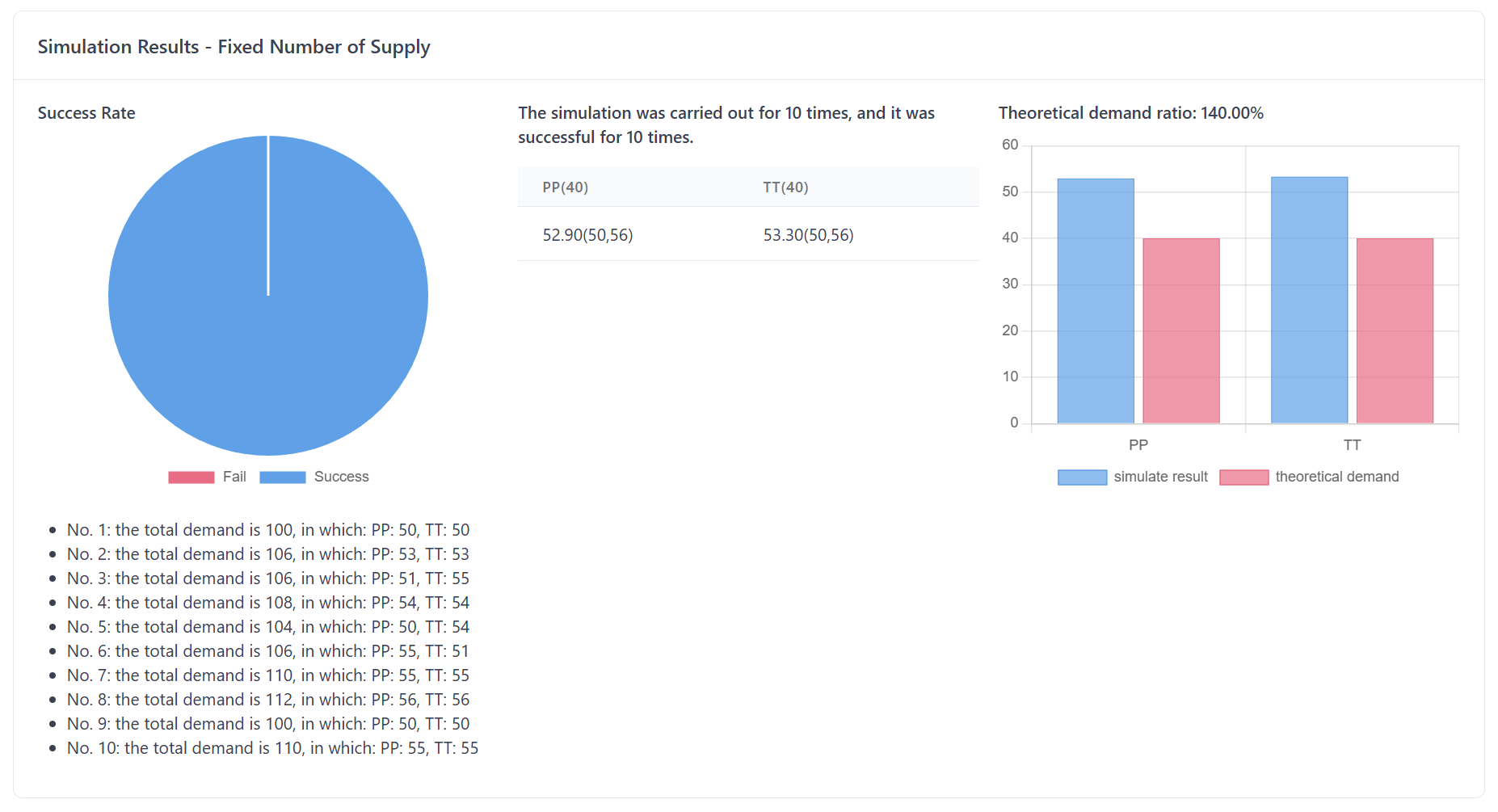
Figure 8. Input Panel

The simulation provides valuable insights to help you assess and refine your material supply strategy. By running multiple iterations, the simulation delivers key outputs that allow you to answer critical questions and make data-driven decisions about trial logistics and material management. Let’s take a closer look at the two main pieces of information the simulation provides:

One of the most critical questions in trial logistics is whether your supply strategy will be able to maintain sufficient stock at each clinical site throughout the trial. The simulation helps answer this question by providing a probability of success that indicates the likelihood that your supply strategy will keep each site adequately stocked.

The probability of success is calculated by running multiple simulations with different random outcomes (e.g., varying patient enrollment rates, treatment allocations, and supply chain conditions). The result reflects the likelihood that the supply strategy you’ve chosen will ensure enough material is available at the centers. The higher the probability of success, the better your supply strategy covers the potential risks. A higher probability means that the strategy is more likely to prevent stockouts, minimize delays, and maintain compliance with the trial protocol. Essentially, a high probability means your material distribution plan is more robust and reliable, while a low probability suggests that the strategy may need adjustments to avoid stock shortages.

In short, this output provides you with a clear picture of whether your supply strategy will be able to meet the demand at clinical sites, given the expected variability in patient enrollment, shipment delays, and other logistical factors.

Another critical output from the simulation is the utility rate of consumption, which compares the actual material consumption (i.e., the amount of product shipped to clinical sites) with the theoretical consumption (i.e., the amount of product actually used by patients in the trial).

Actual Consumption refers to the quantity of material shipped to the clinical centers, which includes both what is used by the patients and any additional materials sent to account for uncertainties (e.g., extra stock for re-dispenses, anticipated losses, etc.). Theoretical Consumption is the estimated amount of material needed based on trial parameters, such as the number of patients, treatment allocation, and visit schedule. Theoretical consumption assumes that there are no discrepancies in patient behavior, no delays, and no unexpected issues with supply.

The ratio of actual consumption to theoretical consumption is a key metric that reflects the efficiency of your supply strategy. The utility rate is calculated conditioned on the coverage of your supply strategy. If the supply strategy has a high coverage (i.e., a high probability of success), the utility rate will give you a better idea of how much excess or shortage of materials there might be, helping you fine-tune your shipping strategy for greater efficiency.

The utility rate helps you understand how efficiently your materials are being used and whether your supply chain is operating in an optimal manner. By assessing the utility rate, you can identify whether you are over-providing materials (leading to waste and inefficiency) or under-providing (leading to the risk of stockouts and disruptions).

Warehouse for Advance Examples